代数方程组

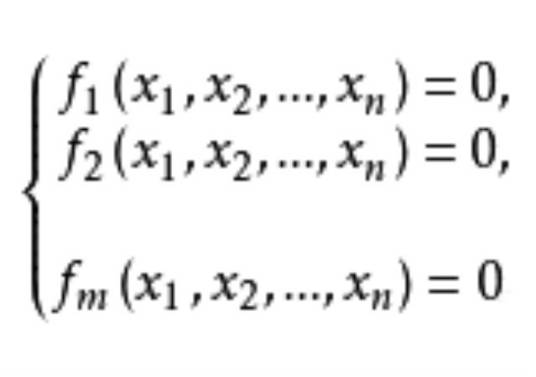
代数方程组(system of algebraic equations)是由多个n元多项式方程所构成的方程组，由数域P上m个n元多项式fi(x1，x2，…，xn)(i=1，2，…，m)组成的方程组称为数域P上的代数方程组，若x1=α1，x2=α2，…，xn=αn满足方程组中的每一个方程，则称它们为代数方程组的一个解。当代数方程组中每个方程的次数≤1时，则代数方程组就是通常的线性方程组；当代数方程组中m=n=1时，代数方程组就是通常的一元n次方程，因此，代数方程组可以看成是线性方程组与一元n次方程的推广和发展，研究代数方程组的解及其性质属于代数几何。在古代巴比伦和1300年前后朱世杰所著《四元玉鉴》中，都曾讨论过二元、三元和四元的高次方程组，但较系统地研究却迟至16世纪，正式讨论已到18世纪，主要由研究高次代数曲线f(x，y)=0，g(x，y)=0的交点数而引起的，贝祖(É.Bézout)于1779年在其所著《代数方程的一般理论》中给出用消元法求解代数方程组的方法 。

想要了解更多“代数方程组”的信息，请点击：代数方程组百科